Answer:
1.6 x 10^21 N
Step-by-step explanation:
The gravitational force can be calculated as
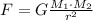
Where G = 6.674 x 10^(-11) m³/kg s². M1 and M2 are the mass and r is the distance between the objects. So, first, we need to convert 143.82 million miles to meters as
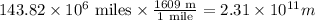
Then, we can replace M1 = 1.99 x 10^30 kg, M2 = 6.42 x 10^23 kg, and r = 2.31 x 10^11 m to get
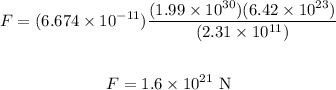
Therefore, the gravitational force is 1.6 x 10^21 N