Question

1. Use the table of the probability distribution to find the variance, o^2A- 0.9B- 3.2C- 0.6D- 9.4

Answer 1

In order to calculate the variance, use the following formula:

`\sum ^n_(n\mathop=1)(\mu-x_n)^(2)P(x_n)`

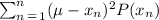
where μ is the mean of the data.

Then, calculate μ:

μ = (1+2+3+4+5)/5 = 3

and replace this value and the values of xn and P(xn) into the formula for the variance, just as follow:

`\begin{gathered} \sigma^2=(3-1)^2(0.06)+(3-2)^(2)(0.14)+(3-3)^(2)(0.43)+ \\ (3-4)^(2)(0.32)+(3-5)^(2)(0.05)=0.9 \end{gathered}`

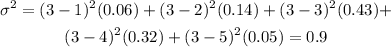
Hence, the variance of the given distribution is 0.9