Answer:
Explanation:
The standard form of a linear equation is
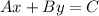
However, it is a lot easier if we find the equation in slope-intercept form

and then rearrange the above equation to write it in standard form.
We are told that the slope of the line is 2/3 which means m = 2/3; therefore, the above equation becomes
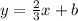
Moreover, fro the point (-5, 1) we know that when x = -5, then y = 1; therefore, the above equation gives
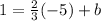
Simplifying the above gives
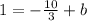
adding 10/3 to both sides gives


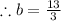
With the value of b in hand, we write the slope-intercept of the equation:
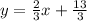
Now, to write the above in standard form, we multiply both sides by 3. This cancels out 3 in the denominator on the right-hand side and gives

Finally, subtracting 2x from both sides gives
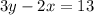
Just shift the position of the terms on the left-hand the side and we get
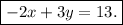
which is the standard form of our equation!