Question

As 20 ft ladder reaches a window 18 ft high. How far is the foot of the ladder from the base of the building? Round your answer to the nearest tenth.

Answer 1

11We are given a problem that can be exemplified in the following diagram:

Since the ladder, the wall and the floor form a right triangle we can use the Pythagorean theorem:

`h^{2^{}}=a^2+b^2`

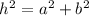
Where

`\begin{gathered} h=\text{hypotenuse} \\ a=\text{height} \\ b=x \end{gathered}`

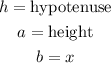
In this case, the hypotenuse is the length of the ladder and the height is the height of the window. Replacing the known values:

`(20)^2=(18)^2+b^2`

Solving the square:

`400=325+b^2`

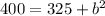
Now we solve for "b", first by subtracting 325 to both sides:

`400-325=b^2`

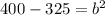
Solving the operation:

`75=b^2`

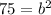
Taking square root to both sides:

`\sqrt[]{75}=b`

Solving the square root:

`8.7=b`

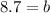
Therefore, the foot of the ladder is 8.7 feet from the building.