Question

1. The masses of largemouth bass, in kilograms, are normally distributed with a mean of 1.1 and a standard deviation of 0.3. Any bass caught with a mass between 0.8kg and 1.7 kg must be released. What percent of the bass does this represent?

Answer 1

Answer:

81.859%

Step-by-step explanation:

The mean, μ = 1.1

The standard deviation, σ = 0.3

Any bass caught with a mass between 0.8 kg and 1.7 kg must be released

P(X₁ < x < X₂) = P(0.8 < x < 1.7)

For X₁ = 0.8, calculate the z-value

`\begin{gathered} z_1=(X-\mu)/(\sigma) \\ \\ z_1=(0.8-1.1)/(0.3) \\ \\ z_1=(-0.3)/(0.3) \\ \\ z_1=-1 \\ \end{gathered}`

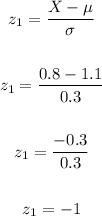
For X₂ = 1.7, calculate the z-value

`\begin{gathered} z_2=(X_2-\mu)/(\sigma) \\ \\ z_2=(1.7-1.1)/(0.3) \\ \\ z_2=(0.6)/(0.3) \\ \\ z_2=2 \end{gathered}`

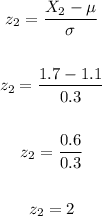
Using the normal distribution table:

P(-1

Percentage of the bass that will be released = 0.81859 x 100%

Percentage of the bass that will be released = 81.859%