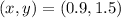Question

Solve the following system using the substitution method. Enter your answer as an ordered pair in the form (x,y). 2x+4y=7.89x-5y=0.6

Answer 1

Given the system of equations:

`\begin{gathered} 2x+4y=7.8\rightarrow(1) \\ 9x-5y=0.6\rightarrow(2) \end{gathered}`

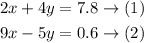
We will solve the system using the substitution method.

Solve the equation (1) for (x):

`\begin{gathered} 2x=-4y+7.8\rightarrow(/2) \\ x=-2y+3.9\rightarrow(3) \end{gathered}`

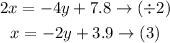
Substitute with (x) from equation (3) into equation (2)

`9(-2y+3.9)-5y=0.6`

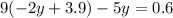
Solve the equation to find (y)

`\begin{gathered} 9\cdot(-2y)+9\cdot3.9-5y=0.6 \\ -18y+35.1-5y=0.6 \\ -18y-5y=0.6-35.1 \\ -23y=-34.5 \\ y=(-34.5)/(-23)=1.5 \end{gathered}`

Substitute with (y) into equation (3) to find (x)

`\begin{gathered} x=-2\cdot1.5+3.9 \\ x=-3+3.9 \\ x=0.9 \end{gathered}`

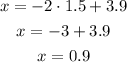
So, the answer will be:

`(x,y)=(0.9,1.5)`