Question

A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h(t) = −4.9t2 + 24t + 7. How long does it take to reach maximum height?

Answer 1

Given:

There are given the equation:

`h(t)=-4.9t^2+24t+7`

Step-by-step explanation:

According to the concept:

For any quadratic function:

`f(x)=ax^2+bx+c`

With the negative leading coefficient, it gets the maximum at:

`x=-(b)/(2a)`

So,

Apply the above formula to the given question.

Then,

From the given function:

`h(t)=-4.9t^(2)+24t+7`

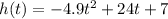
Where,

`\begin{gathered} a=-4.9 \\ b=24 \end{gathered}`

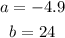
Then,

Put the all values into the given formula:

So,

`\begin{gathered} x=-(b)/(2a) \\ x=-(24)/(-2(4.9)) \\ x=(24)/(9.8) \\ x=2.45 \end{gathered}`

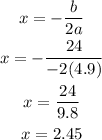
Final answer:

Hence, it will take 2.45 seconds to get the maximum height.