Question

A golfer strikes a golf ball from the top of a 2.3 m tall hill to the green below. The initial velocity of the golf ball is 28 / s / (45 degrees) above the horizontall Determine golf ball's time of flight, range, maximum height and final velocityA. 3s / 13.5 mB. 2s/15mC. 1.32s/12.5m D. 12m

Answer 1

Given:

the initial velocity of the ball is

`u=28\text{ m/s}`

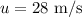
height of the hill is

`h=2.3\text{ m}`

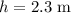
The angle at which the ball is projected

`\theta=45^(\circ)`

Required: time of flight range, maximum height and final velocity is to be calculated.

Step-by-step explanation:

when a ball is struck at an angle

`\theta=45^(\circ)`

with initial velocity u then its velocity has two components that is given by

in y-direction, velocity is

`\begin{gathered} u_y=u\sin\theta \\ u_y=28\text{ m/s }\sin45^(\circ) \\ u_y=19.79\text{ m/s} \end{gathered}`

in x-direction velocity is ,

`\begin{gathered} u_x=u\cos\theta \\ u_x=28\text{ m/s }\cos45^(\circ) \\ u_x=19.79\text{ m/s} \end{gathered}`

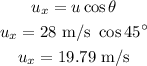
maximum of height of the ball is given by

`h=(u_y^2)/(2g)`

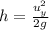
Plugging all the values in the above formula we get,

`\begin{gathered} h=\frac{(19.79\text{ m/s})^2}{2*9.\text{8 m/s}^2} \\ h=19.98\text{ m} \end{gathered}`

time of flight of the ball is given by

`T=(2u_y)/(g)`

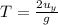
plugging all the values in the above relation we get,

`\begin{gathered} T=\frac{2*19.79\text{ m/s}}{9.8\text{ m/s}^2} \\ T=4.03\text{ sec} \end{gathered}`

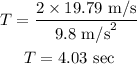
Range of the ball is given by

`R=(u^2*\sin2\theta)/(g)`

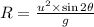
Plugging all the values in the above formula we get,

`\begin{gathered} R=\frac{(28\text{ m/s})^2*\sin90}{9.8\text{ m/s}^2} \\ R=80\text{ m} \end{gathered}`

Thus, range is 80 m, and Time of flight is 4.03 sec and maximum height is 19.98 m.