we have the equation
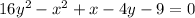
step 1
Group similar terms and move the constant term to the right side
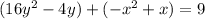
step 2
Factor 16 in the first term and factor -1 in the second term
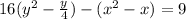
step 2
Complete the square twice

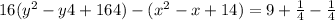
step 3
Rewrite as perfect squares
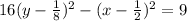
step 4
Divide both sides by 9
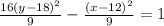
therefore
The answer is Hyperbola