The controller puts money in 3 places.
First,
He puts money at 2% per year
Let it be "x"
The interest accumulated is
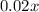
Second, he puts 1/3rd of previous at 3% per year.
That will be investing (1/3)x at 3%
The interest accumulated is
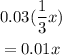
Thirdly, he puts another balance, Let it be "y", at 9% CD.
The interest accumulated is:
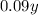
The sum of all the 3 account interest is $603, thus we can write:
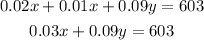
This is equation 1.
Also, we are told that the total amount of investments is 10,000, thus we can write:
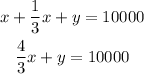
We have to solve these equations simultaneously to find x and y.
Lets solve for y of the 2nd equation and put it into the first equation and solve for x. Shown below:

So, y is:
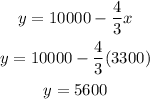
So,
Answer
$3300 invested in first account$1100 invested in second account$5600 invested in third account