Question

Suppose two trains leave Mexico City at the same time. One travels east and the other travels west at a speed that is 10mph slower. In 1.5 hours, the trains are 171 miles apart. Find the speed of the train. Set up a table to help you set up the equation

Answer 1

63 mph and 53 mph

Step-by-step explanation:

We can represent the situation as:

Therefore, if we call x the speed of the train that travels east, (x-10) is the speed of the train that travels west.

Then, after 1.5 hours, they are at a distance of 171 miles and they are getting apart at a speed equal to the sum of both speeds, so we can write the following equation:

`\begin{gathered} \text{speed = }(dis\tan ce)/(time) \\ x+(x-10)=(171)/(1.5) \end{gathered}`

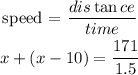
So, solving for x, we get:

`\begin{gathered} x+x-10=114 \\ 2x-10=114 \\ 2x-10+10=114+10 \\ 2x=124 \\ (2x)/(2)=(124)/(2) \\ x=62 \end{gathered}`

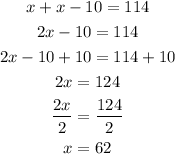
Therefore, the speed of the first train was 63 mph and the speed of the second train was 10 mph slower, so it was 53 mph.