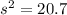Solution
- The formula for finding the variance of the sample dataset is given below:

- The data points have been given to be 12, 14, 19, 11, 8, 21, and 13.
- The formula for finding the Mean is

- Thus, we can simply apply the formula given above to solve the question. We shall follow these steps to solve this question:
1. Find the Mean.
2. Calculate the Variance
1. Find the Mean
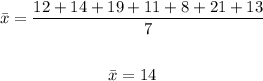
2. Calculate the Variance:

Final Answer
The value of the variance is