Answer:
Let the type A coffee be
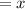
Let the type B coffee be
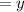
Three times as many pounds of type B coffee as type A, will be represented below as
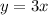
The cost of type A coffee is
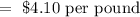
The cost of type B is
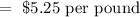
The total cost of both coffee is
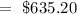
Hence,
The equation will be

Hence,
The number of pounds of type A coffee is = 32 pounds