Question

6. Members of the student council are trying to calculate the budget for Howard's upcoming Howard Idol. Their calculations are based on the ticket price, x. Below are the functions that they came up with: Concert Income: -X2 +20x - 30 Concert Expenses*: 5x + 6 (*Auditorium rental, lights, costumes, snack bar) Profit is calculated by doing Income-Expenses. Write a Profit equation to represent this scenario.b. A break-even point is when zero dollars are made. Find the break-even point.

Answer 1

The total expenses (or costs) for the concert are given by the model:

C(x)=5x+6

Where x is the ticket price

The income (or revenue) is modeled by the function:

`I\mleft(x\mright)=-x^2+20x-30`

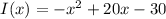
a) The profit is calculated as the incomes minus the costs:

P(x) = I(x) - C(x)

Substituting the above models:

`\begin{gathered} P(x)=-x^2+20x-30-(5x+6) \\ \text{Operating:} \\ P(x)=-x^2+20x-30-5x-6 \\ P(x)=-x^2+15x-36 \end{gathered}`

b) To calculate the break-even point, we equate the profit to zero:

`\begin{gathered} -x^2+15x-36=0 \\ \text{Multiplying by -1} \\ x^2-15x+36=0 \end{gathered}`

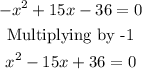
The polynomial can be factored:

( x - 12 ) ( x - 3 ) = 0

We have two solutions:

x=12, x=3

There are two break-even points, when the price is $3 or when the price is $12

.