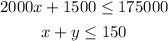Question

Let x be the number of loads by land carriersand y the number of loads by air carriers.Which system of inequalities represents thissituation?A mail distribution center processes asmany as 175,000 pieces of mail each day.The mail is sent via ground and air. Eachland carrier takes 2000 pieces per loadand each air carrier 1500 pieces perload. The loading equipment is able tohandle as many as 150 loads per day.Click on the correct answer.1500x + 2000y 175,000x + y = 1501500x + 2000y s 175,000x + y s 1502000x + 1500y s 175,000x + y = 1502000x + 1500y 175,000x + y 2 150

Answer 1

Consider that 'x' is the number of loads by land carrier, and 'y' is the number of loads by air carrier.

Given that each land carrier takes 2000 pieces per load, the total number of pieces processed in 'x' loads is,

`\begin{gathered} \text{Total No. of mails processed by land carrier}=2000* x \\ \text{Total No. of mails processed by land carrier}=2000x \end{gathered}`

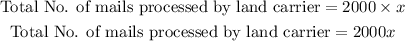
Similarly the total number of mail pieces processed by air carrier in 'y' loads, will be,

`\begin{gathered} \text{Total No. of mails processed by air carrier}=1500* y \\ \text{Total No. of mails processed by air carrier}=1500y \end{gathered}`

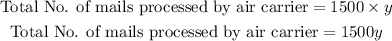
Given that the total number of mails processed each day is at most 175000,

`2000x+1500y\leq175000`

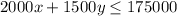
Also there is an upper constraint of 150 on the total number of loads,

`x+y\leq150`

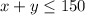
Thus, the given situation can be characterized by following inequations,

`\begin{gathered} 2000x+1500\leq175000 \\ x+y\leq150 \end{gathered}`