Question

Let f(x) = 6x^2 - 4x(a) Find the derivative of the line tangent to the graph of f at x = 2.Slope at x = 2: ___(b) Find an equation of the line tangent to the graph of f at x= 2.Tangent line: y= ___

Answer 1

Step-by-step explanation

We are given the function

`f(x)=6x^2-4x`

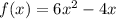
for part A

we are to find the derivative of the line tangent to the graph of f at x = 2

So, we will have

`f^(\prime)(x)=12x-4`

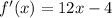
when x =2,

`f^(\prime)(x)=12(2)-4=24-4=20`

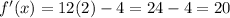
Thus, the slope at x is 20

For part B

To get the equation of the line tangent to the graph at x =2, we will substitute x =2 into f(x)

`f(2)=6(2)^2-4(2)=6*4-8=24-8=16`

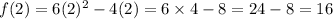
Thus, using the formula

`\begin{gathered} y=mx+c \\ where \\ y=16,\text{ m=20,x=2} \\ 16=20*2+c \\ 16=40+c \\ c=16-40 \\ c=-24 \end{gathered}`

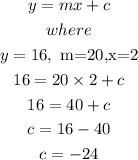
Therefore, the equation is

`y=20x-24`

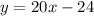
Thus, the tangent line is: y= 20x -24