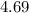Solution:
Given:
![\begin{gathered} y=\sqrt[3]{x-1} \\ on\text{ the interval \lbrack3,6\rbrack} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/njoydkhkzeb8opgtcz8o60zizb1uofpxsq.png)
where a = 3, b = 6, n = 4.
This gives
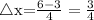
Divide the interval into 4 subintervals of the length Δx with the following endpoints:

For the Left Riemann sum, we evaluate the function at the left endpoints of the subintervals. Thus, we have
sum up the values and multiply by Δx, we have
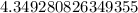
To the second decimal place, we have the Left Riemann sum to be
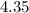
For the Right Riemann sum, we evaluate the function at the right endpoints of the subintervals. Thus, we have
sum up the values and multiply by Δx, we have

To the second decimal place, we have the Right Riemann sum to be