Question

suppose that the time required to complete a 1040R tax form is normally distributed with a mean of 90 minutes and a standard deviation of 10 minutes. What proportion of 1040R tax forms will be completed in more than 77 minutes?

Answer 1

Finding the proportion is the same as finding the following probability:

`P(X\ge77)`

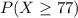
in a normal distribution with mean 90 and standard deviation 10. To find this probability we use the z-score, defined by:

`Z=(x-\mu)/(\sigma)`

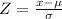
where x is the value we need (in this case x=77), hence the probability we are looking for can be calculated as:

`P(X\ge77)=P(Z\ge(77-90)/(10))=P(Z\ge-1.3)`

Using the tables of a normal distribution we have that:

`P(Z\ge-1.3)=0.9032`

Hence:

`P(X\ge77)=0.9032`

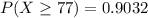
Therefore, 90.32% of tax forms will be completed in more than 77 minutes.