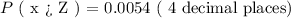SOLUTION:
Step 1:
In this question, we are given the following:
When σ Is Known
If the standard deviation, σ, is known, we can transform to an approximately standard normal variable, Z:
![\text{Z = }\frac{X_i-\mu}{(\frac{\sigma}{\sqrt[]{n}})}](https://img.qammunity.org/2023/formulas/mathematics/college/3euhfl4if4dx1n9bgon2i5ukaq85qj8n63.png)
Step 2:
Now, we have that:
Find the probability that the mean benefit for a random sample of 27 patients is less than $3810.
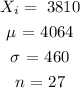
![Z\text{ = }\frac{3810\text{ - 4064}}{\frac{460}{\sqrt[]{27}}}](https://img.qammunity.org/2023/formulas/mathematics/college/93vmbnyc4pf8udvah7fmm0kb4pzl169fe9.png)


Hence,
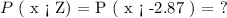
From the Probability table, P(x
![P(x</p><p>Step 3:</p><p></p><p>Find the probability that the mean benefit for a random sample of 27 patients is more than $4290.</p>[tex]\begin{gathered} X_i=\text{ 4290} \\ \mu\text{ = 4064} \\ \sigma\text{ = 460} \\ \text{n = 27} \end{gathered}]()
![Z=\frac{4290\text{ - 4064}}{\frac{460}{\sqrt[]{27}}}](https://img.qammunity.org/2023/formulas/mathematics/college/ko1oijwqf66m1xnvl37uprk47adznxbrku.png)

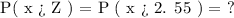
From the Probability table, we have that:
Given Z = 2.55,
P(x>Z) = 0.0053861