Solution:
Given:

step 1: Express each mixed number as improper fractions.
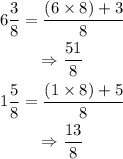
step 2: Find the difference between the fractions.
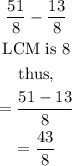
step 3: Expressed the obtained fraction as a mixed number.

Since the result of the above operation is not equal to
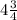
The correct choice is No.
Given:
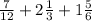
step 1: Express each mixed number as improper fractions.
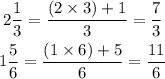
step 2: Find the sum of the fractions.
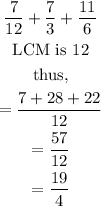
step 3: Expressed the obtained fraction as a mixed number.
Thus,
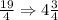
Since the result of the above operation is
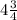
The correct choice is Yes.