We can write a system of equations that satisfy this two conditions:
- No solution
- The slope of one of the equations is 3.
We start with the second condition: we can write the equation of a line with slope 3 as:
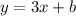
Then, we can assign any value to the y-intercept b, for example b=0, and we have the first equation as:
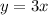
For the system to have no solution, the two equations have to be parallel lines that are not equal.
We can do it by writing a line equation with the same slope m=3, so they are parallel, but with a different y-intercept, like b=1.
Then, we have the equation:
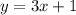
If we graph both equations, we get:
The two lines do not intersect for any finite values of x and y, so the system has no solution.
Answer:
The system of equations:
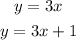
has no solution and a equation with slope 3.