Question

A line passes through the points (12, -1) and (4, -5). Which points lie on the same line? Select all that apply. (6,-3) (0, -7) (-5, 4) (2,-6) (16, 1) (-4, 5)

Answer 1

find the equation of the line that pass through points (12,-1) and (4,-5)

find the slope of the line

`\begin{gathered} m=\frac{_{}y_2-y_1_{}}{x_2-x_1} \\ m=(-5-(-1))/(4-(12)) \\ m=(-4)/(-8) \\ m=(1)/(2) \end{gathered}`

find the y intercept replacing one of the points

`\begin{gathered} y=(1)/(2)x+b \\ -5=(1)/(2)(4)+b \\ -5=2+b \\ -5-2=b \\ -7=b \end{gathered}`

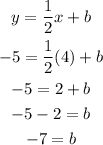
write the complete equation

`y=(1)/(2)x-7`

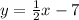
replace the coordinate x of the points into the equation, if y is equal to the coordinate then the points lie on the same line.

when x=6

`\begin{gathered} y=(1)/(2)(6)-7 \\ y=3-7 \\ y=-4 \end{gathered}`

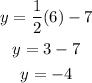
the point (6,-3) does not lie on the same line

when x=0

`\begin{gathered} y=(1)/(2)(0)-7 \\ y=-7 \end{gathered}`

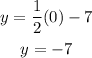
the point (0,7) lies on the same line.

when x=-5

`\begin{gathered} y=(1)/(2)(-5)-7 \\ y=-2.5-7 \\ y=-9.5 \end{gathered}`

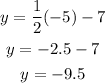
the point (-5,4) does not lie on the same line

when x=2

`\begin{gathered} y=(1)/(2)(2)-7 \\ y=1-7 \\ y=-6 \end{gathered}`

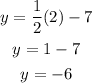
the point (2,-6) lies on the same line

when x=16

`\begin{gathered} y=(1)/(2)(16)-7 \\ y=8-7 \\ y=1 \end{gathered}`

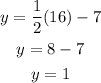
the point (16,1) lies on the same line

when x=-4

`\begin{gathered} y=(1)/(2)(-4)-7 \\ y=-2-7 \\ y=-9 \end{gathered}`

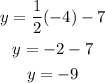
the point (-4,5) does not lie on the same line.

The points that will lie on the same line will be (0,-7);(2,-6);(16,1)