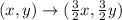Answer::
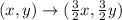
Step-by-step explanation:
From the diagram, we use the point K to find the rule:
• The coordinate of point K is (2,2)
,
• The coordinate of its image K' is (3,3)
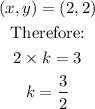
Therefore, the algebraic expression that shows how to find the coordinate of K'L'M' is: