Given the cross sectional area, CSA, of a cylinder to be
![\text{CSA}=32\operatorname{cm}^2]()
The cross section of a cylinder is a circle, thus the formula for the cross sectional area of a cylinder is
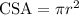
Solving to find the radius of the cylinder below
![\begin{gathered} 32=\pi r^2 \\ \text{Divide both sides by }\pi \\ (\pi r^2)/(\pi)=(32)/(\pi) \\ r^2=(32)/(\pi) \\ \text{Square root of both sides} \\ \sqrt[]{r^2}=\sqrt[]{(32)/(\pi)} \\ r=\sqrt[]{(32)/(\pi)}cm \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k6hq1tnkfletbdqltiojyhyaoyb4ktv8ga.png)
To find the total surface area, TSA, of a cylinder, the formula is
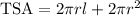
Where
![\begin{gathered} l=\text{length}=25\operatorname{cm}\text{ and } \\ r=\text{radius}=\sqrt[]{(32)/(\pi)}cm \end{gathered}]()
Subsitute the values intom the formula for the total surface area of a cylinder
![\begin{gathered} \text{TSA}=2\pi rl+2\pi r^2 \\ \text{TSA}=2(\pi*\sqrt[]{(32)/(\pi)}*25)+2(\pi*(\sqrt[]{(32)/(\pi)})^2) \\ \text{TSA}=501.3257+64 \\ \text{TSA}=565.3257 \\ \text{TSA}=565.3\text{cm}^2\text{ (nearest tenth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ulddfzgwaevymkc2lykn2kr2cx1spnbn39.png)
Hence, the total surface area of the cylinder is 565.3cm² (nearest tenth)