Question

Find the absolute maximum and absolute minimum of the function

Answer 1

Given data:

The given expression for the function is f(x)=-2sin(x)cos(x).

Th egiven expression can be written as,

f(x)=-sin2x.

Differentiate the given function with respect to x an equate to zero.

`\begin{gathered} f^(\prime)(x)=0 \\ (d)/(dx)(-\sin 2x)=0 \\ -2\cos 2x=0 \\ \cos 2x=0 \\ 2x=(\pi)/(2),\text{ }(3\pi)/(2) \\ x=(\pi)/(4),\text{ }(3\pi)/(4) \end{gathered}`

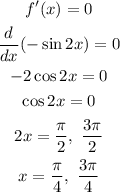
Avoid x=π/4.

The value of function at x=π/3.

f(π/3)=-sin(2π/3)

=-0.866.

The value of at x=3π/4.

f(3π/4)=-sin(6π/4)

=-1

The value of function at x=π is,

f(π)=-sin(2π)

=0

Thus, the maximum value of function is 0 at x=π, and minimum value is -1 at x=3π/4.