we have the expression
x^2+9x+20
Complete the square
equate the expression to zero
x^2+9x+20=0
group terms
(x^2+9x)=-20
x^2+9x+(9/2)^2-(9/2)^2=20
x^2+9x+(9/2)^2=20+(9/2)^2
Rewrite as perfect squares
(x+9/2)^2=-20+81/4
(x+9/2)^2=1/4
take square root on both sides
![(x+(9)/(2))=\pm\sqrt[]{(1)/(4)}](https://img.qammunity.org/2023/formulas/mathematics/college/imnnfmnmrpa2uwr7489gjslpbms2qna236.png)
simplify
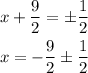
the values of x are
x=-4 and x=-5
therefore
the given expression in factored form is
x^2+9x+20=(x+4)(x+5)
another way to find out the factored form
the formula to solve a quadratic equation of the form
ax^2+bx+c=0
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In this problem we have
x^2+9x+20=0
so
a=1
b=9
c=20
substitute in the formula
![x=\frac{-9\pm\sqrt[]{9^2-4(1)(20)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/fdql0e93j0blqo8s9ncb8702fx2owd5m02.png)
![\begin{gathered} x=\frac{-9\pm\sqrt[]{1}}{2} \\ x=(-9\pm1)/(2) \\ x=(-9+1)/(2)=-4 \\ x=(-9-1)/(2)=-5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dcxr4ituz4rrfvzol7m76rsonvn0zivl02.png)
the values of x are
x=-4 and x=-5
therefore
the factored form is
(x+4)(x+5)