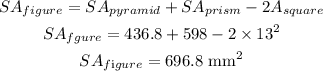Answer
Surface area of pyramid = 436.8 mm²
Surface area of the prism = 598 mm²
Total surface area of the figure = 696.8 mm²
Explanation
The surface area of a pyramid is calculated as follows:
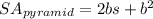
where b is the length of the base, and s is the slant height of the pyramid.
From the diagram, b = 13 mm, and s = 10.3 mm, then:
![\begin{gathered} SA_(pyramid)=2*13\operatorname{*}10.3+13^2 \\ SA_(pyram\imaginaryI d)=267.8+169 \\ SA_(pyram\imaginaryI d)=436.8\text{ mm}^2 \end{gathered}]()
The surface area of a rectangular prism is calculated as follows:
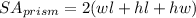
where w is the width, l is the length, and h is the height of the prism.
Substituting w = 13 mm, l = 13 mm, and h = 5 mm, we get:
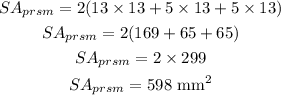
While computing the surface area of the pyramid, we take into consideration the area of the square base.
The area of this same square was considered when computing the SA of the prism (in this case, this square is at the top of the prism)
But, now we need to calculate the SA of the whole figure and this square must not be included (it is not at the surface of the whole figure). Then, to calculate the SA of the whole figure, we need to add the SA of the pyramid to the SA of the prism, and then subtract two times the area of this square with dimensions 13 by 13 mm. That is,