Given: A composite solid
To Determine: The volume of the given solids
Solution
The diameter of the cone is the same as the length of the prism. Therefore, the diameter is 4cm
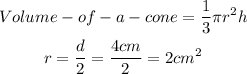
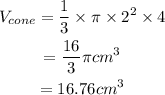
Volume of the rectangular prism is
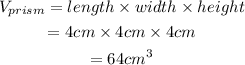
The volume of the composite solid is
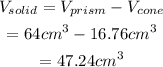
Hence, the volume of the composite solid is 47.24cm³