Question

A piston-cylinder of gas has an initial pressure of 25 psi.  The volume is increased to 2.5 times the initial volume.  The temperature is increased from 290oC to 720oC.  What is the final pressure.  Be careful,.. SYW

Answer 1

We know that the product of pressure and the volume divided by the temperature is a constant if the mass of the gas remain constant, this means that:

`(P_iV_i)/(T_i)_{}_{}=(P_fV_f)/(T_f)`

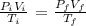
First we need to convert the temperature to the absolute scale:

`\begin{gathered} T_i=290+273.15=563.15 \\ T_f=720+273.15=993.15 \end{gathered}`

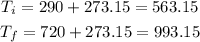
The final volume is 2.5Vi. Plugging the values given and solving for the final pressure we have that:

`\begin{gathered} (25V_i)/(290)=(P_f(2.5V_i))/(720) \\ P_f=(25V_i(993.15))/(2.5V_i(563.15)) \\ P_f=17.64 \end{gathered}`

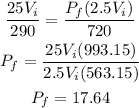
Therefore the final pressure is 17.64 psi.