Question

The school store sells pens for $0.35 each and pencils for $0.15 each. Anthony spent $2.80 to buy a total of 12 pens and pencils. How many pens did Anthony buy?A. 4B. 5C. 6D. 7

Answer 1

Let C be the number of pencils and S the number of pens that Anthony bought.

Since a total of 12 pens and pencils were bought, then:

`C+S=12`

Since Anthony spent $2.80 and each pen costs $0.35 while each pencil costs $0.15, then:

`0.35S+0.15C=2.80`

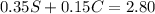
Since we want to know S (the number of pens that Anthony bought), isolate C from the first equation:

`C=12-S`

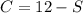
Substitute C=12-S into the second equation:

`0.35S+0.15(12-S)=2.80`

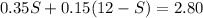
Use the distributive property to rewrite 0.15(12-S) as 0.15*12-0.15S:

`0.35S+0.15\cdot12-0.15S=2.80`

Sum alike terms on the left hand side of the equation:

`0.20S+0.15\cdot12=2.80`

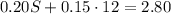
Multiply 0.15*12:

`0.20S+1.80=2.80`

Substract 1.80 from both sides of the equation:

`0.20S=2.80-1.80`

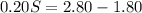
Simplify the sum on the right hand side of the equation:

`0.20S=1.00`

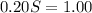
Divide both sides by 0.20:

`S=(1.00)/(0.20)`

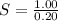
Simplify the fraction:

`S=5`

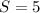
Therefore, Anthony bought 5 pens.