since they are similar triangle, we have
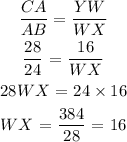
To solve for AD
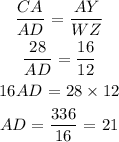
To solve for YZ
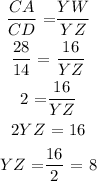
To solve for XZ, I will have to get the angle, given, check out this diagram.
From the diagram, i have to find, the value of X using cosine rule, which becomes.
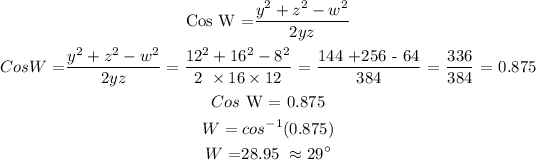
Then to find XZ? we shall use cosine rule
![\begin{gathered} XZ^2=WZ^2+WX^2\text{ - 2(}WZ\text{)(}WX\text{) COSXZ} \\ XZ^2=12^2+16^2\text{ - 2}*12*16\text{ COS 29} \\ XZ^2\text{ = 144 + 256 -384(0.874)} \\ XZ^2\text{ = 400 - 335.6} \\ XZ^2\text{ = 64.384} \\ XZ\text{ = }\sqrt[]{64.384\text{ }}\text{ = 8cm} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zjsby1ao0364nb4c64udnfr5qqrdmqfzti.png)
To find DB?
