The Law of Sines
It's an equation that relates the lengths of the sides of a triangle with the sines of its angles.
For the given triangle, the equation is:
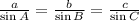
a.
We are given: m/_A = 80°, m/_C = 33°, and c=45.1.
We use the first and the last part of the equation above:
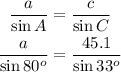
Solving for a:

Calculating:
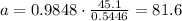
a = 81.6
b.
Now we are given m/_B=48°, m/_C=26°, a=19.9
Since we are required to calculate the value of c and we are not given the value of the angle A, we first determine it recalling the sum of angles of a triangle is 180°, thus:
m/_A= 180° - 48° - 26° = 106°
Now we apply the equation:
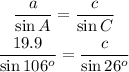
Solving for c:

c = 9.08