Question

The center of the circle is at point (0,4). The point (-6, 4) is on the circle. What is the radius of the circle?

Answer 1

We are given the coordinates of the center and one point of a circle. To determine the radius we must determine the distance between the two points. To do that we will use the following formula:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Where:

`\begin{gathered} (x_1,y_1)=(0,4) \\ (x_2,y_2)=(-6,4) \end{gathered}`

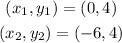
Replacing in the formula for the distance:

`d=\sqrt[]{(-6-0)^2+(4-4)^2}`

Solving the operations:

`\begin{gathered} d=\sqrt[]{(-6)^2+0^2} \\ d=\sqrt[]{36} \\ d=6 \end{gathered}`

Therefore, the radius of the circle is 6.