Question

Can I get help with this? calculate the volume and the area of the figure

Answer 1

The surface area of the cone is 373.66 cm^2 and the volume is equal to 366.19 cm^3

Explanation:

Given:

Radius (r) = 7 cm

Slant height (s) = 10 cm

To calculate the surface area of a cone we apply the following formula:

`\begin{gathered} A_S=\pi\cdot r^2+\pi\cdot r\cdot s \\ \\ \text{ We replacing:} \\ \\ A_S=\left(3.14\right)\left(7\right)^2+\left(3.14\right)\left(7\right)\left(10\right) \\ \\ A_S=153.86+219.8 \\ \\ A_S=373.66\text{ cm}^2 \end{gathered}`

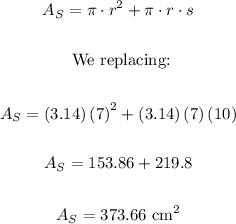
To calculate the volume of a cone, we calculate it by the following formula:

`V=(1)/(3)\pi\cdot r^2\cdot h`

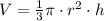
To calculate the volume we must determine the height of the cone, we do it by means of the Pythagorean theorem, where the hypotenuse is the slant height and one of the sides is the radius, like this:

`\begin{gathered} c^2=a^2+b^2 \\ \\ \text{ we replacing} \\ \\ 10^2=7^2+h^2 \\ \\ h^2=100-49 \\ \\ h=√(51) \\ \\ h=7.14\text{ cm} \end{gathered}`

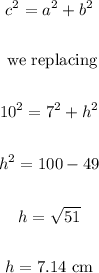
Now if we substitute to calculate the volume:

`\begin{gathered} V=(1)/(3)(3.14)(7)^2(7.14) \\ \\ V=366.19\text{ cm}^3 \end{gathered}`

The surface area of the cone is 373.66 cm^2 and the volume is equal to 366.19 cm^3