Question

Find the area of the circle and the area of the sector round your answer to the nearest tenths

Answer 1

Area of the circle

The are of a circle is given by:

`A(\text{circle) = }\pi\cdot r^2`

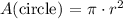
Where:

π = 3.14159

r = radius of the circle

In our problem we have:

r = 5

So, applying the formula of above we find that:

`A(\text{circle) = }\pi\cdot5^2\cong78.5398\cong78.5`

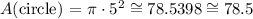
Circle Area = 78.5 mi²

Area of the sector area of the circle

We can calculate the area of a sector of a circle using the following formula:

`A(\text{sector) = }\pi\cdot r^2\cdot(\theta)/(360)`

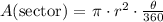
Where:

θ = angle of the sector

In our problem we have:

θ = 60°

So, applying the formula of above we find that:

`A(\text{sector) = }\pi\cdot5^2\cdot(60)/(360)\cong13.0899\cong13.1`

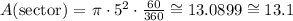
Sector Area = 13.1 mi²