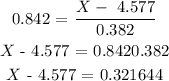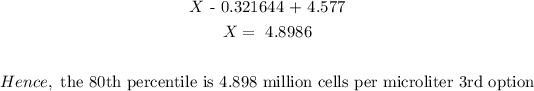Question

Assume that the red blood cell counts of women are normally distributed with a mean of 4.577 million cells per microliter and a standard deviation of 0.382 million cells per microliter. Find the 80th percentile for the red blood cell counts of women. Round to three decimal places.options:4.6554.8784.898

Answer 1

Answer:
`\text{the 80th percentile is 4.898 million cells per microliter \lparen3rd option\rparen}`

Step-by-step explanation:

Given:

mean = 4.577 million cells per microliter

standard deviation = 0.382 million cells per microliter

To find:

the 80% percentile for the red blood cell counts of women

To determine the 80th percentile, we will apply the z-score formula:

`\begin{gathered} \begin{equation*} z=(X-μ)/(σ) \end{equation*} \\ \sigma\text{ = 0.382} \\ \mu\text{ = 4.577} \\ X\text{ = ?} \\ z\text{ = z-score of 80\% percentile} \end{gathered}`
`\begin{gathered} Using\text{ z-score percentile for normal distribution} \\ The\text{ z-score of the 80th percentile = 0.842} \end{gathered}`

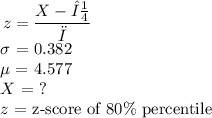
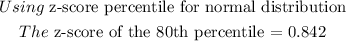
substitute the values:

`\begin{gathered} 0.842\text{ = }\frac{X-\text{ 4.577}}{0.382} \\ X\text{ - 4.577 = 0.842\lparen0.382\rparen} \\ X\text{ - 4.577 = 0.321644} \end{gathered}`
`\begin{gathered} X\text{ - 0.321644 + 4.577} \\ X=\text{ 4.8986} \\ \\ Hence,\text{ the 80th percentile is 4.898 million cells per microliter \lparen3rd option\rparen} \end{gathered}`