We need to determine which of the given points lies on the circle with the equation:
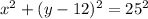
In order to do so, we can replace x with the first coordinate of the point, and y with the second coordinate and see if the equation holds true.
A. For the point (20,-3), we have:
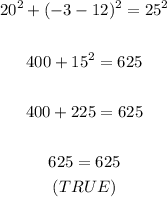
Therefore, point (20,-3) lies on the circle.
For the other points, we have:
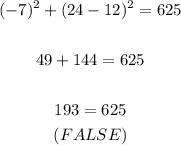
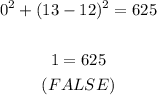
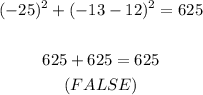
Therefore, the only correct option is A: (20,-3).