Question

There are 8 athletes at a track meet. How many different ways can they finish first orsecond?

Answer 1

Since we have 8 athletes, we have 8 possible choices for the person that will be the first place.

Then, after choosing the first place, there will be 7 athletes left for the second place, so the second place has 7 possible choices.

To find the number of different ways, let's multiply the number of possible choices for each position:

`8\cdot7=56`

We can also calculate this value as a of 8 choose 2:

`\begin{gathered} A(n,p)=(n!)/((n-p)!) \\ A(8,2)=(8!)/(6!)=8\cdot7=56 \end{gathered}`

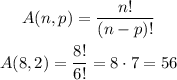
Therefore there are 56 different ways.