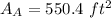Answer:
The surface area of cone A is;
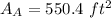
Step-by-step explanation:
Given that the scale factor of cone A to cone B is;
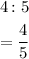
If the surface area of cone B is 860 ft^2;
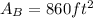
The since they are similar, the surface area of the two cones can be related using the formula;
![\begin{gathered} (4)/(5)=\sqrt[]{(A_A)/(A_B)} \\ ((4)/(5))^2=(A_A)/(A_B) \\ (A_A)/(A_B)=(16)/(25) \\ A_A=(16)/(25)A_B \\ A_A=(16)/(25)(860) \\ A_A=550.4\text{ }ft^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dxjfh85yhtwi4odajtcbfw1dwuo3tku0ix.png)
Therefore, the surface area of cone A is;