Let's find each side first
Using the distance formula
B(-2,-4), C(3, 3),
![BC\text{ = }\sqrt[]{(3+2)^2+(3+4)^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1s8je3yvtjnnc11utnz3cmq3itaxd8pldd.png)
![=\sqrt[]{5^2+7^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/nasghmrc0f88g334880cag2d0m7pedp3e0.png)
![=\sqrt[]{25+49}](https://img.qammunity.org/2023/formulas/mathematics/high-school/d31k7f1w947m8v79oqkzsjfhhx1x71o0bc.png)
![=\sqrt[]{74}](https://img.qammunity.org/2023/formulas/mathematics/high-school/zl8xpdx0v9s7jpm8t72aoa87qcav27yayb.png)
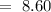
C(3, 3), D(-2, 3)
![CD\text{ =}\sqrt[]{(-2-3)^2+(3-3)^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/k5s34t047rleudibjpr50ovlygxm7747tm.png)
![=\sqrt[]{25}](https://img.qammunity.org/2023/formulas/mathematics/college/fc2icqz090b1hpyylhkts3m6fckigcnxg4.png)
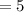
D(-2, 3) B(-2,-4)
![DB=\sqrt[]{(-2+2)^2+(-4-3)^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/8hokh91vczot1nklhrkxto3rxk8mgbxgoy.png)
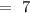
Now, to find the angles, use the cosine formula
BD = c = 7
BC = d = 8.6
CD = b =5
Using the formula;
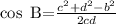
substitute the values into the formula and evaluate
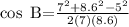
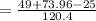
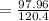
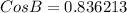
Take the cos ⁻ ' of both-side
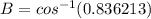
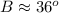
To find angle C, we will use the cosine formula
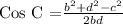
substitute the values and evaluate
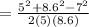
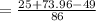
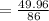
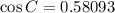
Take the cos ⁻ ' of both-side
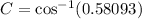
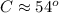
To find the third side
B + C + D = 180° (sum of angle in a triangle)
36 + 54 + D = 180°
90 + D = 180°
D = 180° - 90°
D = 90°