Question

What is the area oft irregular shape? 6 ft square f f 3 ft 8 ft 16 ft

Answer 1

hello

to solve this question, we need to solve each object separately. i.e the triangle and the rectangle separately.

`\begin{gathered} \text{area of the triangle =}(1)/(2)b* h \\ \text{area of the rectangle = l}* w \end{gathered}`
`\begin{gathered} \text{width(w)}=(3)/(2)=1.5ft \\ \text{height}=6ft \\ \text{area of the triangle = 2}*\text{(}(1)/(2)*1.5*6) \\ \text{area of the triangle= 9ft}^2 \end{gathered}`

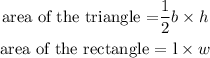
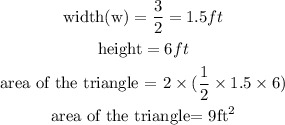
area of the rectangle is

`\begin{gathered} a=l* w \\ l=8ft \\ w=16ft \\ a=8*16 \\ a=128ft^2 \end{gathered}`

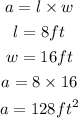
now the total area of the irregular object is equal to the sum of the area of the triangle + area of the rectangle

`\begin{gathered} \text{area}=9+128 \\ \text{area}=137ft^2 \end{gathered}`

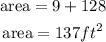
from the calculation above, the area of the irregular shape is 137 squared feet