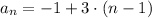The expression of the n-th term of an arithmetic sequence is
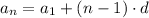
The problem here is to find the initial value a1 and the value of d (common difference), then, let's write that equation for each value that we have, first, let's do n = 5
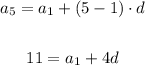
Now let's repeat the process for n = 11
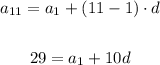
Now we have a system of equations!
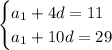
To solve that system we can subtract the equations
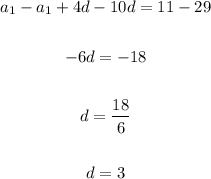
We can find a1 now because we have the value of d, we can use any of the two equations we wrote to do it, I'll use the first one
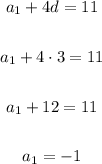
Now we have all the term to write the rule of the n-th term,
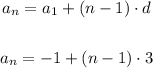
The rule for the n-th term is