Question

The points P(2, -3), Q(3,-2) and R(8,k) are collinear, find the value of k

Answer 1

`k=3`

Step-by-step explanation: We have to find the missing number k, the three coordinate points are as follows:

`\begin{gathered} P(x_1,y_1)=(2,-3) \\ \\ P(x_2,y_2)=(3,-2) \\ \\ P(x_3,y_3)=(8,k) \end{gathered}`

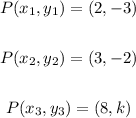
The general equation of the line can be determined as follows:

`\begin{gathered} y(x)=mx+b \\ \\ m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(-2-(-3))/(3-2) \\ \\ m=(-2-(-3))/(3-2)=(1)/(1)=1 \\ \\ y(x)=x+b \\ \\ -3=2+b\rightarrow b=-5 \\ \\ y(x)=x-5\rightarrow(1) \end{gathered}`

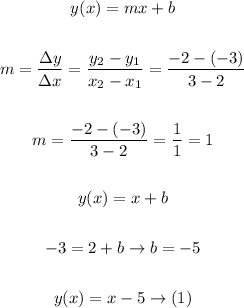
Using equation (1) and plugging in the value of x the unknown k is calculated as follows:

`\begin{gathered} P(x_(3),y_(3))=(8,k) \\ \\ x=8 \\ \\ k=y(8)=8-5=3 \\ \\ k=3 \end{gathered}`

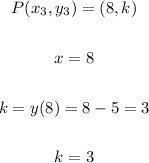
Graph confirmation:

The graph indeed verifies the answe