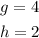Given the System of Equations:
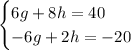
You can solve it using the Elimination Method:
1. You can identify that the first term of the first equation and the first term of the second equation is equal but they have opposite signs. Then, you can cancel them by adding the equations:
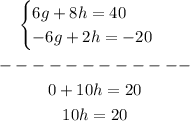
2. Solve for "h":
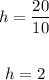
3. Substitute the value of "h" into one of the equations and solve for "g":
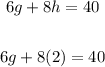
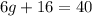
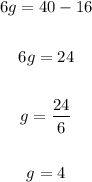
Hence, the answer is: