Question

I have completed the first three parts of this question, but now need help to finish...I need to calculate the ratios of the 4 line segments LK, LM, ON, and OP. Based on the ratios, what can you conclude about three or more parallel lines that intersect two transversals?

Answer 1

At first, we will find the lengths of LK, Lm, ON, OP, then use them to find the ratios between them

The rule of the distance is

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

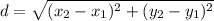
For LK

Since L = (3, 6), K = (1,5.33), then

`\begin{gathered} LK=√((3-1)^2+(6-5.33)^2) \\ LK=√(4+0.4489) \\ LK=√(4.4489) \end{gathered}`

For LM

Since L = (3, 6), M = (5, 6.67), then

`\begin{gathered} LM=√((3-5)^2+(6-6.67)^2) \\ LM=√(4+0.4489) \\ LM=√(4.4489) \end{gathered}`

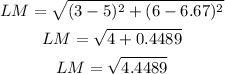
For ON

Since O = (3, 2.59) and N = (5, 4.2), then

`\begin{gathered} ON=√((3-5)^2+(2.59-4.2)) \\ ON=√(4+2.5921) \\ ON=√(6.5921) \end{gathered}`

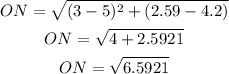
For OP

Since O = (3, 2.59), P = (1, 0.99), then

`\begin{gathered} OP=√((3-1)^2+(2.59-0.99)^2) \\ OP=√(4+2.56) \\ OP=√(6.56) \end{gathered}`

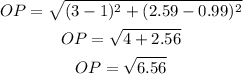
Now let us find the ratios between them

`\begin{gathered} (KL)/(LM)=(√(4.4489))/(√(4.4489))=1 \\ (PO)/(ON)=(√(6.56))/(√(6.5921))=0.9975\approx1 \\ (KL)/(LM)=(PO)/(ON)=1 \end{gathered}`

That means, Parallel lines intercept equal parts

By joining MP

We will have Triangle KPM

Since KL = LM ------- Proved using the distance formula

Since LQ // KP ------ Given

Then MQ = QP ------- Using the theorem down

The theorem

If a line is drawn from a midpoint of one side of a triangle parallel to the opposite side, then it will intersect the 3rd side in its midpoint (Q is the midpoint of MP)

Parallel lines intercept equal parts