Question

I want to solve the problem by using these numbers1,2,2,4,6,7,7, 8, 9and here is the question(__) + (__) ÷ (__) = 2 × + +(__) - (__) + (__) = 5 - + +(__) + (__) + (__) = 13 = = = 15 15 15

Answer 1

- Let the numbers be:

a1 + a2 ÷ a3 = 2

x + +

a4 - a5 + a6 = 5

- + +

a7 + a8 + a9 = 13

= = =

15 15 15

- Now let us write ou the possible equations:

`\begin{gathered} a_1+a_2/ a_3=2 \\ a_1+(a_2)/(a_3)=2\text{ \lparen Equation 1\rparen} \\ \\ a_4-a_5+a_6=5\text{ \lparen Equation 2\rparen} \\ \\ a_7+a_8+a_9=13\text{ \lparen Equation 3\rparen} \\ \\ a_1* a_4-a_7=15 \\ a_1a_4-a_7=15\text{ \lparen Equation 4\rparen} \\ \\ a_2+a_5+a_8=15\text{ \lparen Equation 5\rparen} \\ \\ a_3+a_6+a_9=15\text{ \lparen Equation 6\rparen} \end{gathered}`

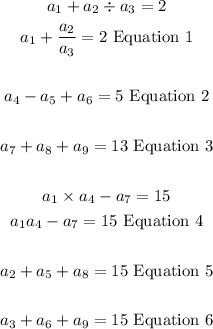
- I do not think this will get us anywhere very quickly.

- Guessing the numbers, we have that:

The ways to get the first horizontal equation are:

The first horizontal equation equates to 2. This means that the equation is essentially 1 + 1 since there are no negative operations. So we have:

1 + 2 / 2 = 2

1 + 7 / 7 = 2

The second horizontal equation equates to 5. There is an addition and a subtraction. Only two sets of positive integers add up to 5. 2 + 3 or 1 + 4. Some other equations exist: -2 + 7 and -4 + 9 and -3 + 8 and -1 + 6

This makes the possibilities for this second horizontal equation greater.

The third horizotal equation equates to 13. All additions. this means that we can have:

6 + 7 = 2 + 4 + 7

5 + 8 = 1 + 4 + 8

4 + 9 = 2 + 2 + 9 = ...

The first vertical equation equates to 15.

The first two numbers multiply and the result is subtracted from a number to get 15.

- We must subtract an odd number from an even number to get an odd number(15).

- Thus, the possibilities of the result of the product are:

(15 + 7), (15 + 1), (15 + 9) = 22, 16, 24

- 22 is out of it since none of the numbers given multiply to give 22.

- 16 = 2 x 8

24 = 6 x 4

- The first horizontal row establishes that the first number must be a 1. However, there is no way to fit a 1 in the first cell in the vertical column. as we just showed.

- Because of these, I do not think the values given work.