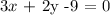SOLUTION:
Step 1:
In this question, we are given the following:
Which equation represents the line passing through the point (-5, 12) and perpendicular to the line y=2/3x +14 ?
Step 2:
The details of the solution are as follows:
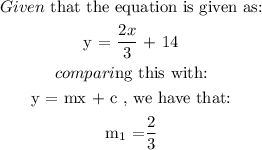

Step 3:
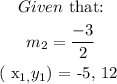
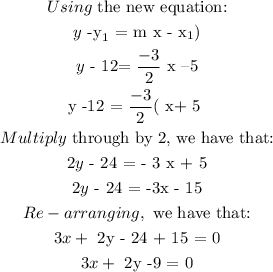
CONCLUSION:
The final answer is: