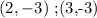
Step-by-step explanation
Step 1
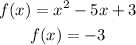
there is a value for y, that is the same for both equations, so
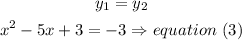
solve equation (3)
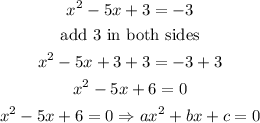
hence, we can use the quadratic formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{replace} \\ x=\frac{+5\pm\sqrt[]{(-5)^2-4\cdot1\cdot6}}{2\cdot1} \\ x=\frac{+5\pm\sqrt[]{25-24}}{2} \\ x=\frac{+5\pm\sqrt[]{1}}{2} \\ x=(+5\pm1)/(2) \\ x_1=(5+1)/(2)=(6)/(2)=3 \\ x_2=(5-1)/(2)=(4)/(2)=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/km16gbfer3z9x3jlxwqyl0tc9nbjvel7hk.png)
so, we have 2 values for x ( 2 and 3)
Step 2
now, find the images
a) when x= 3
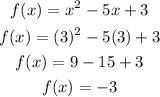
b) when x= 2
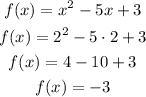
therefore the solutions are
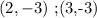
I hope this helps you