First way. Distribute the 5 first.
In this way, we first remove the parentheses and isolate x later
By multipliying 5 by the term into the parentheses, we get
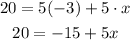
Now, if we move -15 to the left hand side as +15, we have
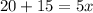
which gives
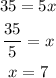
that is, x is equal to 7.
Second way. Divide by 5 first
In this way, we first move 5 to the left hand side and isolate x later
If we move 5 to the left hand side, we have
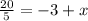
which gives
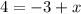
if we move -3 to the left hand side as +3, we obtain
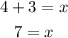
so, we obtain the same result, x=7.