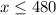Solution:
Given:
40kg crates to be loaded on a shipping container which can load a maximum of 25,000kg.
The container already has 5800kg of other shipments loaded on it.
Each crate weighs 40kg
The number of 40kg crates is represented by x.
Hence, the total weight of the crates to be loaded is;
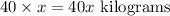
The inequality can be given by;

Therefore, the inequality is;
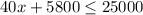
To solve for the number of crates;
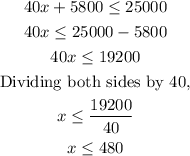
Therefore, the number of 40kg crates that can be loaded into the shipping container can not exceed 480 crates.
Hence, a maximum of 480 40kilogram crates can be loaded on the shipping container alongside other shipments weighing 5800kg.
Thus, the inequality to determine the number of 40kg crates is;